应用数学与交叉科学研究中心数学与纤维材料团队在2023年10月19日上午10:00于崇真楼3028教室进行每周小组组会,小组全体成员和各位导师共同参加。在这次组会上,由一名研三和两名研二的员工分别汇报自己的研究进展,然后老师与同学们对汇报内容进行学术探讨,并对存在的问题给出相应的指导和建议。
— 员工汇报内容展示 —
谢磊:本次组会介绍了受损树状分叉网络中自发渗吸的分形模型。
自发渗吸因其在自然界的广泛存在而引起了人们的广泛关注。在本研究中,我们从理论上探讨了受损v形树状分支网络的自发渗吸现象。此外,吸胀能力由两个无因次量表征:吸胀势和吸胀时间。然后使用分形理论生成这两个无量纲量的解析表达式。在此基础上,系统研究了结构参数对渗吸过程的影响。分支数N对吸胀势有明显的增强作用。引入了参数平面来可视化参数组合,从而能够直接评估特定网络系统中的吸胀过程。该模型揭示的物理机制为受损树状网络的渗吸过程分析提供了有效的指导。


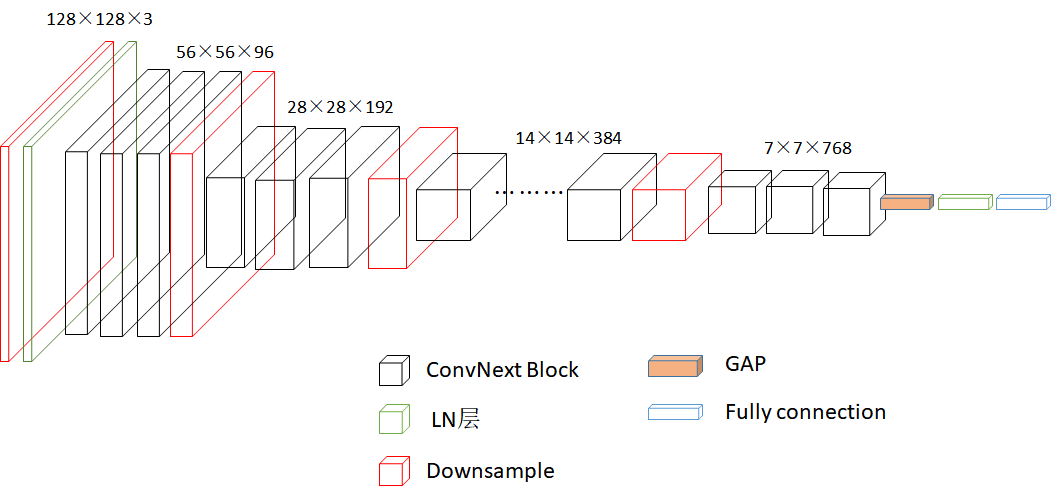
刘博:本次组会介绍了ConvNext的应用与改进。ConvNext是在卷积网络领域足以媲美注意力机制模型的网络,其主要结构由深度可分离卷积、GeLU激活函数、全连接层、LayerNorm归一化层构成。在实际应用中,不同的数据集图像特征不同,特别是在卫星图像数据集中,因为其类间多样性大、类内相似性大从而导致模型提取特征困难,进而不得不考虑更改模型结构以适应不同的数据集。以BN替换LN,Relu替换GeLU,SSCOnv替换深度可分离卷积,让模型提取的特征更倾向于卫星图像数据是一种有效的手段。经过实验,改进后的模型在精度上提升10.8%,但参数量略有增加。

杨淮:今日组会讲述了关于分数阶微积分猜想问题的证明思路,关于定理中的右侧既对于分形连续函数的阶黎曼-刘维尔积分图像的上盒子维数是不超过函数图像的盒子维数。文章中对于函数在定义区间上的变差做分割通过放缩以及积分中值定理得到了小分割上的上界,并且是对于任意的正阶次的黎曼刘维尔积分算子都是满足的。对于猜想的左侧估计,杨淮同学借助豪斯多夫维度与盒子维数的关系对构造的豪斯多夫维数小于的情况进行讨论,对覆盖进行放缩得到新的豪斯多夫测度,在保证豪斯多夫维度存在的情况下可以推导出关于分数阶积分的阶次是小于的。这就相当于证明了猜想的必要性。并且对与定理的充分性给出了两种证明思路。

